hypray2
hypray2
hypray2 allows one to observe a 3D curved and regularly tesselated space on a screen. High-resolution in-depth images take a few seconds to be rendered. However, for lower resolution the program is able to render many images per second in real time allowing one to navigate through a curved space and choose a view of the space, like in a 3D videogame.
Whereas the mathematical core of hypray2 was created as hypray1 more than 20 years ago by Niklas Beisert, hypray2 is originated as a project for the Night of Physics 2022 at ETH Zurich. Since hypray1 various additions and upgrades has been made, including better computational performance, graphics and gui.
hypray2 as well as this web page are work in progress. All updates will be posted on this webpage.
Das Programm hypray2 ermöglicht es, einen optischen Eindruck regelmäßg geteilter gekrümmter Räume zu berechnen und diesen auf einem Bildschirm darzustellen. Hochaufgelöste Bilder mit Blick weit in den Raum hinein benötigen durchaus einige Sekunden Rechenzeit. Für geringere Auflösungen jedoch läßt sich das Programm auch dazu benutzen, viele Bilder pro Sekunde in Echtzeit ausrechnen zu lassen: so kann man - wie in einem 3D-Spiel - durch einen gekrümmten Raum gleichsam navigieren und bestimmen, wohin man fliegen und aus welcher Perspektive man den gewählten gekrümmten Raum betrachten möchte.
Während der mathematische Kern von hypray2, die Berechnung der Darstellung hyperbolischer Geometrien, als hypray1 schon vor mehr als 20 Jahren von Niklas Beisert programmiert worden ist, entstand hypray2 als Projekt für die Nacht der Physik 2022 an der ETH Zürich. Neben grafischer Benutzeroberfläche und effizienter Speicherung von Bildern, Geometrien, Perspektiven und Flügen sind es vor allem zahlreiche neue technische Möglichkeiten wie Parallelisierung und Multithreading, die zu einer deutlich verbesserten Grafikleistung führen.
hypray2 sowie diese Webseite sind noch in Arbeit. Alle Aktualisierungen werden auf dieser Webseite veröffentlicht.
Raytracing
Raytracing
When tracing rays, the light rays a traced backward from the lens of the camera to the light sources and the color and brightness of each pixel on the screen are determined. While in the flat space the light travels in straight lines, in curved space rays follow the so-called geodesics. Apart from that, the principle of raytracing remain the same.
Beim Raytracing verfolgt man die Strahlen von der Lichtquelle zum Auge bzw. zur Kamera rückwärts und bestimmt so Farbe und Helligkeit jedes Pixels der Bildebene. Während im flachen Raum die Lichtstrahlen auf Geraden verlaufen, folgen sie in gekrümmten Räumen sogenannten Geodäten. Ansonsten bleibt das Prinzip des Raytracings dasselbe.
Mirror Box
Spiegelbox
If the considered space has regular structures embeded (such as tiling), ray tracing can be simplified by using a mirror box. The walls of the fundamental cell are provided with mirrors and the structure visually copies itself infinitely often, like in a kaleidoscope. In our case the fundamental cell is a simplex with adjustable angles at the edges.
Hat der betrachtete Raum eine regelmässige Struktur (Kachelung, Packung), kann man das Raytracing durch Benutzung einer Spiegelbox vereinfachen. Dabei werden die Wände einer Fundamentalzelle der Geometrie mit Spiegeln versehen und somit -- wie bei einem Kaleidoskop -- die Struktur unendlich oft visuell kopiert. Bei uns ist die Fundamentalzelle ein Simplex (Dreieckspyramide) mit frei justierbaren Winkeln an den sechs Kanten.
curved space
gekrümmter Raum
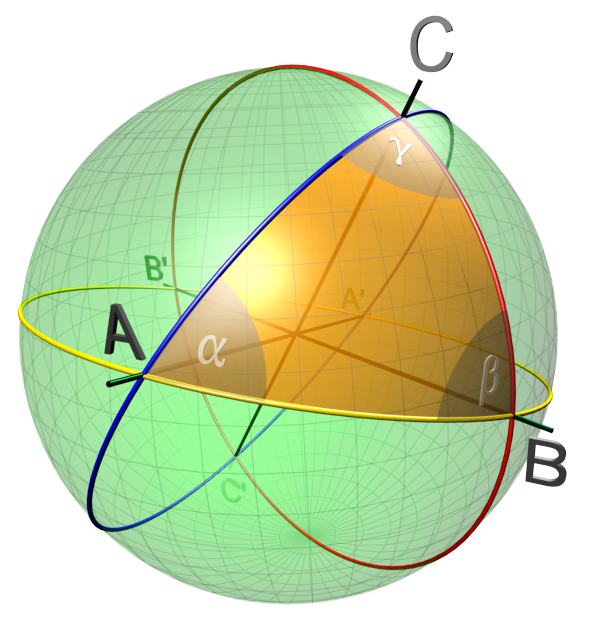
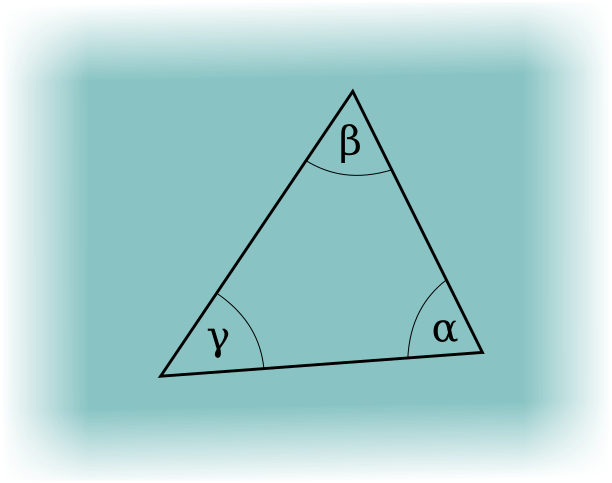
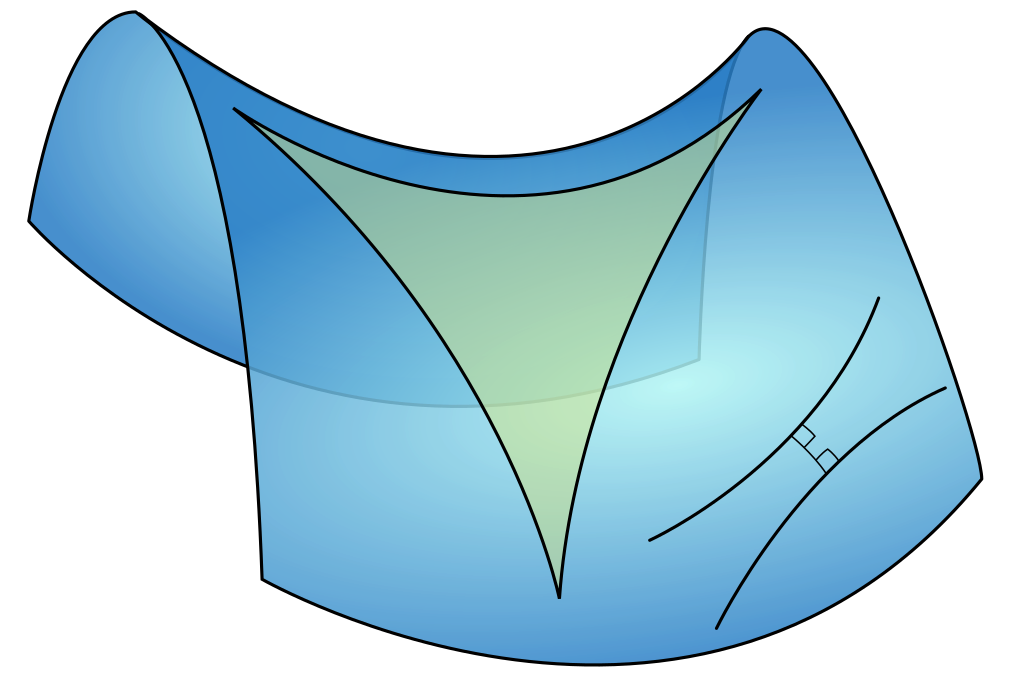
We percept the space we live in as a flat 3D space. In two dimensions the curvature can be easily determined by measuring the sum of interior angles of a triangle. In flat space the sum is always 180 degrees, in sperical space the sum is always greater than 180 degrees (positive curvature) and in the hyperbolic space the sum is less than 180 degress (negative curvature).
In unserer Wahrnehmung leben wir in einem flachen Raum: Geraden, die an einer Stelle parallel zueinander verlaufen, tun dies auch, wenn man sie unendlich weit in ihrem Lauf verfolgt. Die Krümmung eines (zweidimensionalen) Raumes läßt sich leicht durch das Messen der Innenwinkelsumme eines Dreiecks bestimmen: addieren sich die Innenwinkel zu 180 Grad, handelt es sich um einen flachen Raum. Ist die Innenwinkelsumme größer als 180 Grad, dann handelt es sich um ein sphärisches Dreieck, die dazugehörige Fläche (die Kugeloberfläche) hat eine positive Krümmung. Ist die Innenwinkelsumme kleiner als 180 Grad, dann spricht man von einem Raum negativer Krümmung, einem hyperbolischen Raum.
regular tesselations
regelmäßige Teilungen
Schläfli symbols
Schläfli-Symbole
A regular tesselation of a space with a regular polyhedron can be described in terms of Schläfli symbols (i1, i2, ..., in). They describe a regular polyhedron in n + 1 dimensions. The Schläfli symbol is defined recursively: (k) symbol describes a k-sided regular polygon, (k,l) symbol describes a polyhedron with l k-sided regular polygon as faces around each vertex, (k,l,m) symbol describes a polytope with m (k,l) polyhedra at each edge, etc.
Eine regelmäßige Aufteilung eines Raumes in reguläre Polyeder kann durch Schläfli-Symbole der Form (i1, i2, ..., in) beschrieben werden. Sie beschreiben einen regulären Polyeder in n + 1 Dimensionen. Schläfli-Symbole werden rekursiv definiert: Das Symbol (k) beschreibt ein k-seitiges reguläres Vieleck, das Symbol (k,l) bezeichnet einen Polyeder, bei dem l k-seitige reguläre Vielecke an jeder Ecke zusammentreffen. Das Symbol (k,l,m) beschreibt ein Polytop with m (k,l) polyedern an jeder Ecke usw.
Tesselations of 2D space
Teilungen des 2D-Raums
To describe a tesselation of a 2D space it is enough to use a Schläfli symbol (i,j). The symbol is understood as follows: the first number i denotes the number of sides of the polygon used to tesselate the plane and the second number j denotes the number of polygons at each vertex. However, only particular Schläfli symbols implement a tesselation for a given space.
For the spherical 2D space there exist only 5 tesselations, which are related to the
Platonic solids:
For the flat space there are only 3 regular tesselations with Schläfli symbols
Finally, the 2D hyperbolic space can accomodate any tesselation (i,j) not mentioned above.
Um eine Zerlegung eines zweidimensionalen Raumes zu beschreiben, genügt das Schläfli-Symbol (i,j). Wie oben erwähnt, gibt die erste Zahl i die Anzahl der Seiten des Polygons an, das als Baustein für die Zerlegung der Ebene genutzt werden soll und die zweite Zahl j bestimmt die Anzahl der Polygone an jeder Ecke. Nicht alle Schläfli-Symbole bezeichnen eine mögliche Teilung eines vorgegebenen Raumes.
Für den sphärischen zweidimensionalen Raum gibt es lediglich 5 Zerlegungen, die zu den fünf platonischen Körpern gehören:
Im flachen zweidimensionalen Raum gibt es drei Zerlegungen mit den Schläfli-Symbolen (3,6), (6,3), (4,4), die zu den Kachelungen aus Dreiecken, Sechsecken und Quadraten gehören.
Der zweidimensionale hyperbolische Raum erlaubt sämtliche anderen Zerteilungen (i,j).
Tesselations of 3D space
Teilungen des 3D-Raums
In order to describe a tesselation of a 3D space, we can consider 2 tesselations of a 2D spherical space, one corresponding to a common polyhedron (k, l) and another to a common vertex (n, m) (if we blow-up the vertex to a sphere). Since the l faces of the common polyhedron split the vertex sphere according to the n edges of the vertex polyhedron, we have to fix l = n. Therefore, a 3D tesselation can be described by the Schläfli symbol (k, l, m). This picture can be generalized by allowing (k, l) and (l, m) to be tesselations of not only a sphere, but also a plane or hyperbolic space. Then we loose the intuative picture we had before, but the tesselations can be constructed anyways.
For the 3D sphere there are six non-trivial tesselations: (3,3,3), (4,3,3), (3,3,4), (3,4,3), (5,3,3), (3,3,5).
The flat 3D space can be tiled with only one shape: cubes, the corresponding symbol is (4,3,4).
The 3D hyperbolic space allows all other possible symbols that were not mentioned earlier.
Zerteilungen eines dreidimensionalen Raumes können auf zwei Zerteilungen eines zweidimensionalen sphärischen Raumes zurückgeführt werden: das zur ersten Zerteilung gehörige Schläfli-Symbol (k,l) beschreibt hierbei einen gewöhnlichen Vielflächner, während das zweite Schläfli-Symbol (n,m) einen gewöhnlichen Vertex beschreibt, den man sich als zu einer Kugel aufgeblasen vorstellen kann. Da die l Flächen des gewöhnlichen Vielflächners die Vertexkugel entlang der Kanten ihrer Zerlegung zerteilen, muss l=n gelten.
Demnach kann die Zerlegung eines dreidimensionalen Raumes durch das Schläfli-Symbol (k,l,m) beschrieben werden.
Diese Methode kann verallgemeinert werden, wenn man für (k,l) und (m,n) nicht nur sphärische Zerteilungen erlaubt, sondern auch solche, die flache und hyperbolische Räume zerlegen. Das eben beschriebene intuitive Bild geht hierbei verloren; dennoch kann die Zerlegung aber konstruiert werden.
Für einen dreidimensionalen sphärischen Raum existieren sechs nichttriviale Zerlegungen: (3,3,3), (4,3,3), (3,3,4), (3,4,3), (5,3,3), (3,3,5).
Ein flacher dreidimensionaler Raum kann nur auf eine Art und Weise zerlegt werden: durch Würfel. Das dazugehörige Schläfli-Symbol lautet (4,3,4).
In einem dreidimensionalen hyperbolischen Raum lassen sich Zerlegungen zu allen anderen Schläfli-Symbolen realisieren.
pictures
Bilder
Examples of images rendered with hypray2 (click on image to open full size):
Die folgenden Bilder sind mit hypray2 gerendert worden (Doppelklick, um das Bild in voller Größe zu öffnen):
movies
Filme
Here you can find examples of movies that can be rendered using hypray2 (double-click on video to open full screen):
Hier gibt es einige Filme, die mit hypray2 gerendert worden sind (Doppelklick, um das Video im Vollbildmodus anzusehen):